During the previous two articles within the mini-series, we discussed data and how we represent data in computer memory as well as how computer systems represent numbers and texts. This article will be the continuity in the series and will briefly discuss the representation of Sounds and Colors in a computer system.
As we have discussed so far, computers work in a binary form, and every data should be converted to a binary format to be processed by computers. That rule also applies to Sounds and Colors. What differed is the way or mechanisms of representation. Let’s see each of the representations one by one as follows:
Sounds
Sound is a vibration that vibrates at a frequency that our (human) eyes cannot notice. Sometimes it is used to measure how fast something is; by saying “something runs by this much sound speed”. Many of us came across the following picture representing sound waves.
The above pictures tell us that each sound has a frequency as a wave length and amplitude. Amplitude means how loud the sound is. Sound waves vary continuously; this means that sound is a continuous value. If something is a continuous value, we can only represent it in an analogous form. To represent sound, we employ a mechanism called ADC (Analogue to Digital Converter).
What ADC does is take a sample of a sound wave and measure it in correspondence to time and amplitude. ADC measures how high the sound’s loudness is in a specified given time interval.
The sound waves are sampled at regular time intervals to convert the analog data to digital. The amplitude of the sound cannot be measured precisely, so approximate values are stored. If we take a sound sample at a reasonably long time interval, our ADC will give us a low-quality value representation. But if we decrease the time interval, the quality of representing the sample sound will get higher drastically. Let me show you what I mean through the following pictures to clarify the concepts.
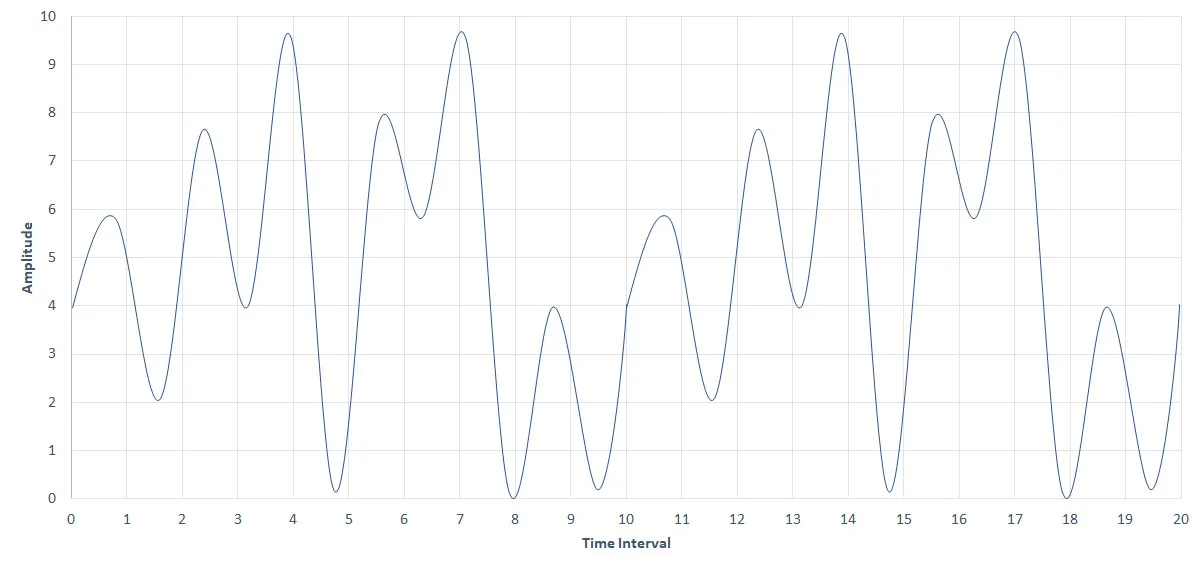
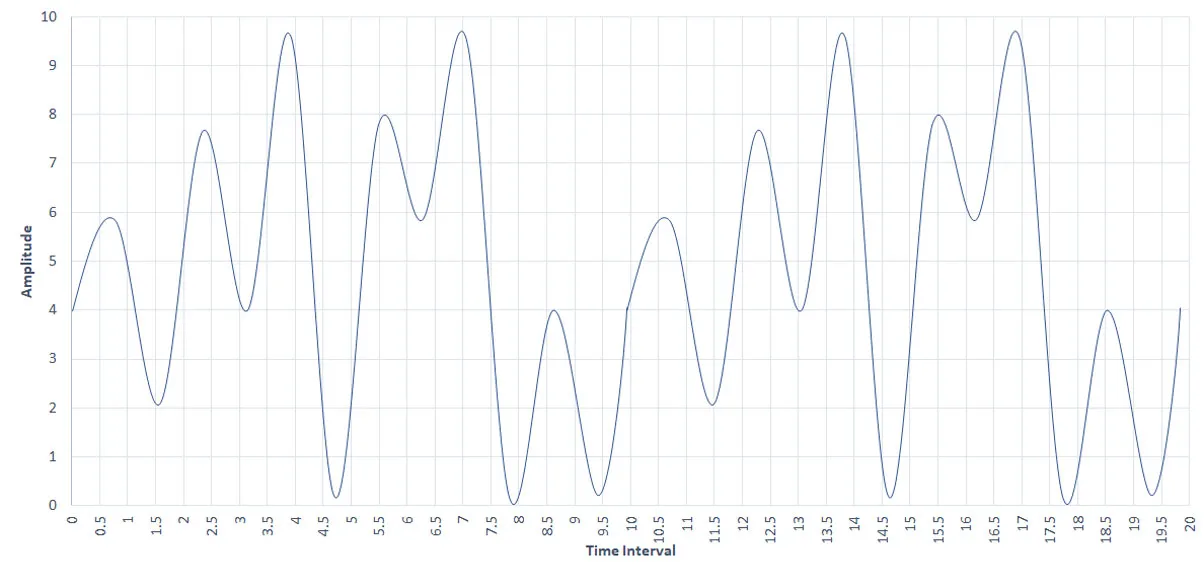
The above pictures illustrate how ADC measures amplitude within a given time interval. The first one takes a sample at a dispersed time interval, i.e., it takes an amplitude sample every one second, but the second takes an amplitude sample every half a second creating a massive difference between the quality of representing the same sound sample.
To familiarize you with terminologies used in sound representation, the number of samples taken per second is known as the Sampling rate. Sampling rate is measured in Hertz (Hz), where 1Hz means ‘One sample per second.’ In our case, the above first graph has a sampling rate of 1Hz, but the second one has 2Hz.
If we take each of the above representations and try to draw a graph to see how good our representation looks, we will get the following result.
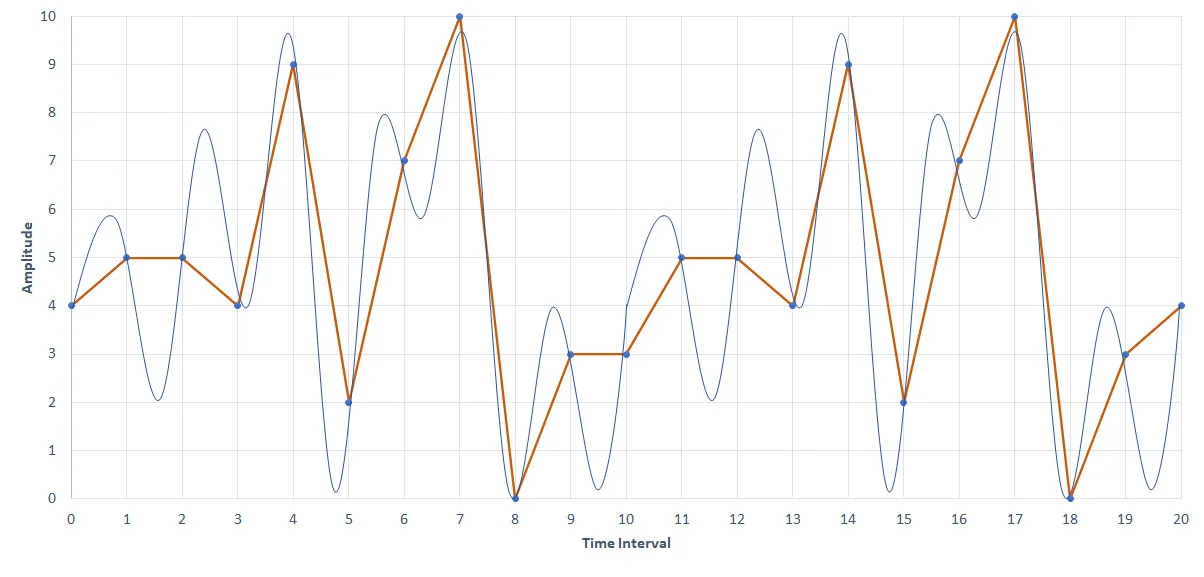
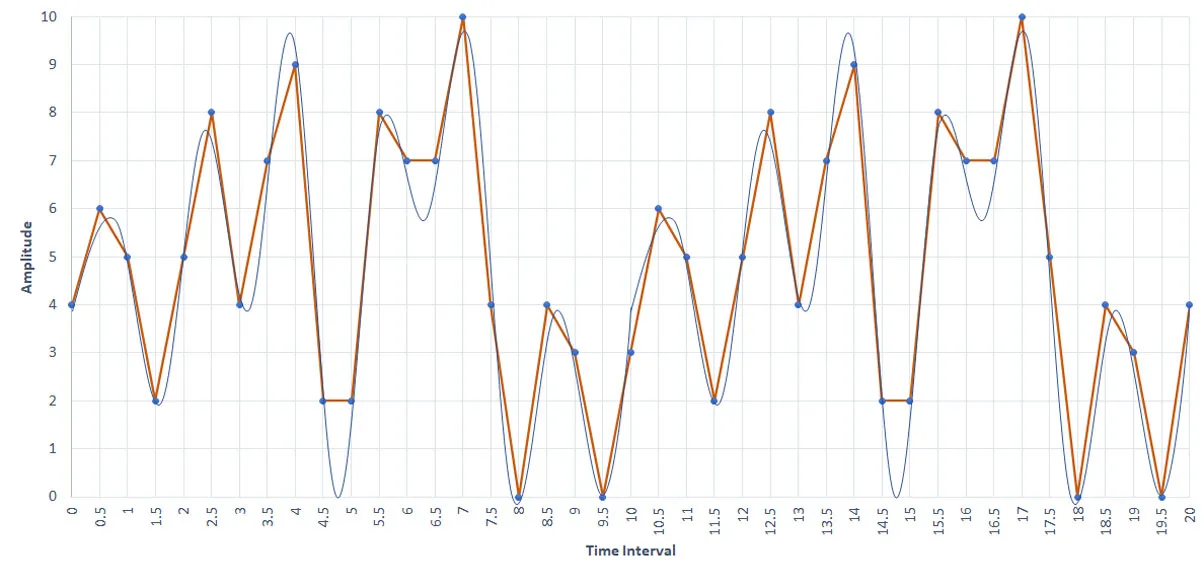
Our thick orange lines clearly show that our half a second sampling is by far better than a second interval sampling. If you ask me, “As the sampling interval gets lower and lower, don’t the file size get higher?” Apparently yes, that’s the cost we need to pay to get an accurate sound sample. The next question might be, “How will I represent this in binary?“. Let’s see how we do it together:
As we have seen in the above graphs, the highest number to represent the maximum loudness of the sample sound is 10, which means our sample sounds amplitude never exceeds 10. This will answer the question, “How many binary positions do we need to represent a single sample value at some specific sample time?”; in our case, we need 4bits. So, the above sound (the sample with a 2Hz sampling rate) will be represented in a series of 4bit binary numbers, for example:
0100 0110 0101 0010 0101 1000 0100 0111 1001 0010 0010 1000 0111 0111 1010 0100 0000 ...The number of bits per sample is called the sampling resolution or bit depth.
Colors
When we talk about colors, we say green, blue, red, and yellow, and while we are mentioning their names in our mouths, their picture will pop into our minds. Since computers treat colors as binaries, their memory cannot recall what the colors look like because it is just a binary number like the rest of the data that can be represented in a computer system. Now, the question is, “How do we represent them in a computer system?“.
To represent a color in a computer system, we need to answer “how many bits do we need to store color?” as we have done so far for the others. To answer that, we need to answer the question “How many colors do we want to represent in our computer system?” which will answer both questions.
If we want to represent only two colors, let’s say white and black, we only need a one-bit binary value; 1 for white and 0 for black, which will give us the basic formula of 2x = n colors. In this case, 2x = 2 colors, so the value for x will be 1, i.e., we need 1 bit to represent two colors. If we want to express 8 different colors, the value for x will be 3 since 23 is equal to 8. The number of bits used to represent each color is called the Color Depth.
We all know that in the natural world, colors are the combinations of 3 primary and different colors; those are Red, Green, and Blue. Combining these 3 different colors will give us billions of different and unique colors. The logic is, how do we represent this natural world scenario in a computerized system in the way mentioned above.
In the early days of the computerization era, colors used to be represented by an 8-bit binary number which will give us 256 different grayscale colors (shades of grays) ‘00000000’ being completely black and ‘11111111’ being completely white. Look at the following picture to grasp what I am talking about, along with the color depth concept.

The above representation of colors can’t address the need to represent billions of colors. So, to address the problem, each of the primary colors will have its own 8-bit binary representation. All other colors will be formed by combining the preceding three primary colors that will give us a massive size of 24-bit (3 * 8) space to represent a single color, allowing us to express billions of colors.
Colors in the computer system will be represented in different formats; the most common ones are the followings:
- RGB tuple value (R, G, B), each one of them ranging from 0 - 255
- Hexa-Decimal value #RRGGBB each one of them taking two hexadecimal places
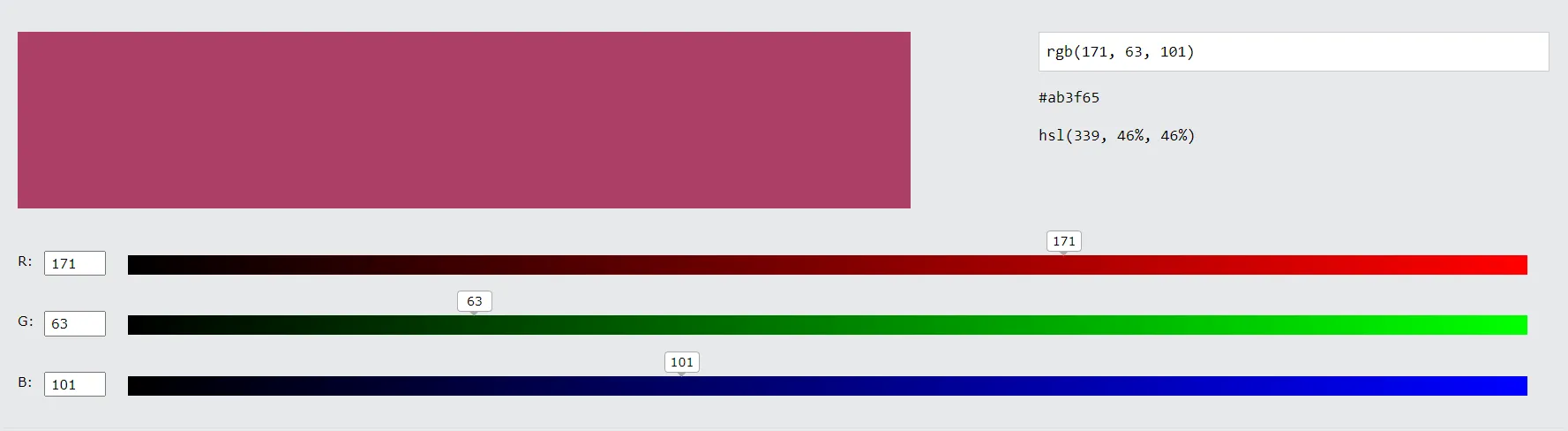
If we want to represent black, we will turn off all 24-bits, resulting in the value of (0, 0, 0) or #000000. If we want to represent white, we need to turn on all 24-bits, resulting in the value of (255, 255, 255) or #FFFFFF. The following picture demonstrates what I am talking about:
In general, this is how we represent Sounds and Colors in a computer system. In the following article, we will try to see how we can represent images and videos in a computer system clearly. Until then, take care!


